Learn about the quadratic equation axis of symmetry and get enhance your understanding of the graphical representation of the equation. Here in the article, we shall discuss the graphical representation of the quadratic equation.
- Roots of Quadratic Equation
- Quadratic Equation Questions
- Standard form of a quadratic equation
- quadratic equation formula
- Sum product of Quadratic equation roots
- Difference between linear quadratic equations
The quadratic equation is the equation that has the standard form of ax^2+bx+c=0. The equation has the x as the unknown numbers and the a,b,c as the standard coefficients. The value of the coefficient is always known in the quadratic equation and with that, we determine the value of x.
Quadratic Equation Axis of Symmetry
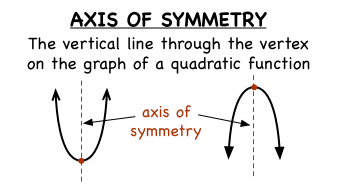
The quadratic equation coefficient is mainly concerned with the graphical representation of the equation. The graphical representation of the quadratic equation is helpful when the standard quadratic formula doesn’t work. In the graphical representation, we basically plot the date on coordinates and axis. The graphical representation of the quadratic equation is known as the parabola.
So, basically, the axis of symmetry is the line when the parabola remains in symmetrical form. It’s basically one of those forms that the quadratic equation may form on its graphical representation. It’s the virtual line that divides the parabola into two halves. In this graphical representation, the symmetry axis always passes through the parabola vertex.
For instance, if we have the stand quadratic equation as y = ax^2+bx+c then we will have the axis of symmetry as x = (-b/2a). So, in a similar way, we may have a different axis of symmetry as per the prevailing equation. Furthermore, in the graphical representation of the quadratic equation, the vertical parabola will mean vertical symmetry. You may check the several other examples and questions based on the Quadratic Equations.

Graphing Quadratic Equations Axis of Symmetry
Well, the symmetry of the axis for the parabola is basically the movement of data on a quadratic equation. It helps us in plotting the data on the quadratic equation graph and subsequently solving the equation. So, in a given quadratic equation you will have to always find the axis of symmetry for the parabola.
You will subsequently use the resulting value on plotting the data and completing the quadratic equation graph. We highly recommend our readers learn the calculation of axis symmetry in the course of a quadratic equation graph. It will always be helpful in the preparation of the overall graphical representation of quadratic equations.