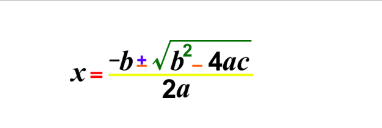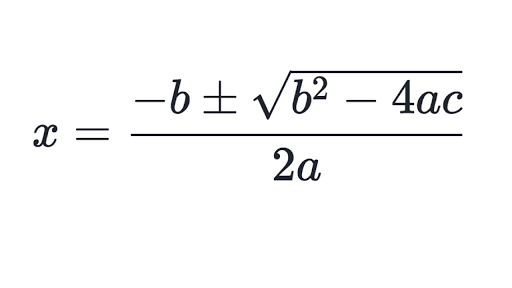Quadratic Equation

Hello friends! Quadratic equations are an integral part of mathematics which has application in various other fields as well. Hence we have made this site to explain to you what is a quadratic equation. After understanding the concept of quadratic equations, you will be able to solve quadratic equations easily.

Now let us explain to you what is a quadratic equation. It is a mathematical equation with the highest power of 2. It is in the form of ax² + bx + c. Here x represents the unknown value, and a, b and c represents known numbers. The solutions of quadratic equations can be using the quadratic formula. There are other methods of finding the solutions of quadratic equations too, such as factoring, completing the square, or graphing. Since quadratic equations have the highest power of 2, there will always be two solutions for x that would be coming up. These values of x that satisfy the equation, are called roots or zeroes of the equation. Hence a quadratic equation will always have two roots or solutions

Here through this article, we have tried to explain to you all concepts of quadratic equations. If you are a student, then learning about these concepts is very important since it will help you solve the problems at school. It is an important concept which has a wide range of application in fields such as physics, chemistry, engineering, etc.

Equation Definition with Quadratic Formula

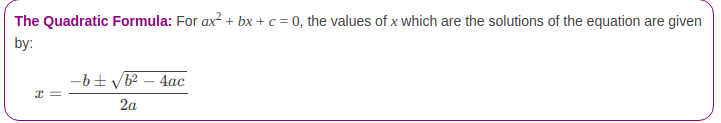
We have discussed with you the general format of the quadratic equation. Now if you require to solve the quadratic equation, you have to use the quadratic formula. Any quadratic equation has two solutions or roots. So you would obtain two roots, one in “+” and one in “-“, and both are the solutions to the equation.

Here we have provided you with a table showing the quadratic formula, so it will be easy for you to memorize and apply it.

Quadratic Equation Calculator

A quadratic equation calculator is a special calculator, which is used to solve the complex quadratic equations. While a scientific calculator might be used to calculate the roots of a quadratic equation, it is always not a convenient method. Hence many online sites online provide quadratic equation calculator which are very easy to use. You just need to enter the known values of a, b and c. It will calculate the roots of the quadratic equations automatically.

Here we have provided you with the quadratic equation calculator where you just need to enter the coefficients of the quadratic equation.

Quadratic Equation Worksheets PDF

Even if you know how to solve the quadratic equations well, you need to practice solving it in order to get hold of the concept. As students, practicing a topic is important for being perfect in it. Hence you can assess how much have you learned about quadratic equations by solving the problems in this worksheet.

This sheet is provided in PDF format so you can take a printout of it and carry it with you anywhere.

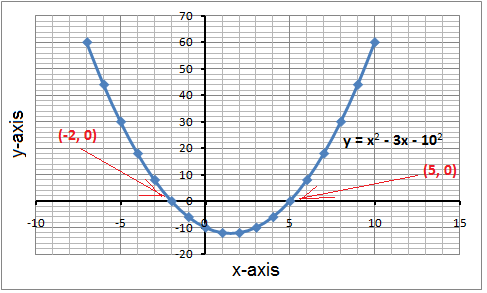
Quadratic Equation Graph

A quadratic equation graph is a graph depicting the values of all the roots of the quadratic equation. Since there are both negative and positive roots of a quadratic equation, the graph takes the shape of a parabola. Hence you can plot a quadratic equation graph by finding different roots of x that solve equality.

To help you understand the quadratic equation graph better, we have provided you with a quadratic equation graph which will help you understand how you can plot a quadratic equation graph.

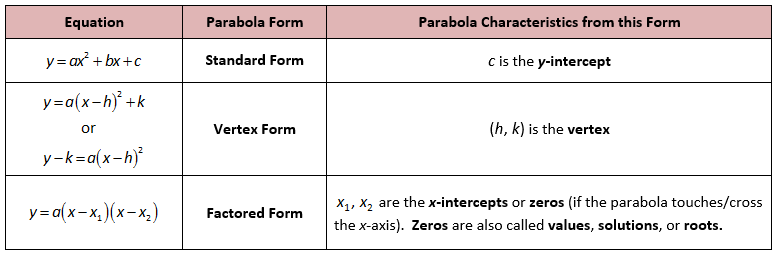
Standard Form of a Quadratic Equation

The standard form of quadratic equation is the equation in form of ax² + bx + c = 0. Here x is the unknown value, and a, b and c are variables. But sometimes, the quadratic equations might not come in standard form, and we might have to expand it.

Here we have provided you with a table showing examples of different forms of quadratic equations, such as vertex form and factor form.

The vertex form of a quadratic equation is given by :

f (x) = a(x – h)² + k, where (h, k) is the vertex of the parabola.

The factored form of a quadratic equation tells us the roots of a quadratic equation. It is written in the form of a⋅(x−p)⋅(x−q) or a⋅(x−p)2

Discriminant of a Quadratic Equation

In mathematics, a discriminant is a polynomial function of its coefficient, which allows us to have an idea of some of the properties of the roots without computing them. Hence in case of a quadratic equation, the discriminant is the part of the quadratic equation underneath the square root. It helps us to determine the number of roots for the quadratic equation.

Here we have provided you with an example of the discriminant of a quadratic equation.

How To Solve a Quadratic Equation

As you know, a quadratic equation is a polynomial with the degree 2. There are various methods through which a quadratic equation can be solved. Following are the methods of solving a quadratic equation :

Factoring

Let us see how to use the method of factoring to solve a quadratic equation.

For example, let us solve the equation (x+4) (x-3) = 0

We will keep the value of each factor as 0.

(x+4) = 0 and (x-3) = 0

Hence, x+4 – 4 = 0 -4 ; or x-3+3 = 0+3

x= -4 or x= 3

2. Completing the Square

Sometimes, some quadratic equations can be factored as perfect squares.

For example, the quadratic equation x²+6x+5 is not a perfect square. But if we add 4 to it, it will become a perfect square. And the resultant expression we would get is (x+3)².

3. Quadratic Formula

This is the most common method of solving a quadratic equation. It involves using the quadratic formula to find the solution or the roots of the quadratic equation.

Given below is the quadratic formula used for solving any quadratic equation :

4. Graphing

Using this method, all the roots of a quadratic equation can be obtained by substituting any value for x which solves the equality.

Before solving a quadratic equation graphically, we must understand what is x-intercept and y-intercept. X-intercept refers to the roots of the quadratic equations that intercept the graph at the X-axis. Similarly, Y-intercept refers to the roots of the quadratic equation that intercepts the graph at Y-axis. The significance of x and y-intercepts is that they depict the roost or the solution of the quadratic equation. You can use any value for x-intercept to find different values of the y-intercept and plot the corresponding points on the graph.

Using the Quadratic Formula

We have told you the various methods through which you can find the solutions of quadratic equations. While the other commonly used methods such as factoring and graphing can be used to find solutions to quadratic equations, the process might get complicated and the result also might not be accurate.

Hence the most preferred method of solving a quadratic equation is using the quadratic formula.

The quadratic formula is given in the form :

Here we shall explain to you how you can apply the quadratic equation for solving problems. You can follow these step-by-step guide to solve any quadratic equation :

For example, take the quadratic equation x² + 2x + 1 = 0

Now let us find the discriminants of the equation :

Discriminant formula = b² − 4ac

Applying the value of a,b and c in the above equation :

22 − 4×1×1 = 0

Now apply the quadratic formula :

x = (−2 ± √0)/2 = −2/2

Therefore, x = -1

Quadratic Equation Solver

Often we come across complex quadratic equations solving which can be tricky and involve complex calculations. Also, there is a risk of the result being wrong. So you can take help of a quadratic equation solver which is basically a quadratic equation calculator.

This calculator is simple to use and will provide you with the correct results in seconds. You just need to enter the coefficients for a,b and c and it will automatically find the value of both the roots of the quadratic equations for you.

To explain to you how you can solve quadratic equations online using the quadratic equations solver, here we have provided you with a video.

Conclusion

Hence through this article, we have tried to explain to you all the concepts of quadratic equations and the various methods through which you can solve them. Using methods such as factoring and graphing, you can easily find the solutions of any quadratic equation. But the most preferred method which can be used to solve any quadratic equation is the quadratic formula. We hope that this article has helped you understand quadratic equations better and enable you to solve any quadratic equation easily.