Mastering Quadratic Equations: A Comprehensive Guide to Boosting Math Confidence

Mastering quadratic equations requires a thorough understanding of the concepts and a step-by-step approach to solving problems.

Quadratic Equations

Here’s a comprehensive guide to help you conquer quadratic equations:

Step 1: Understand the Basics

Before diving into problem-solving, it’s crucial to establish a firm grasp of the fundamental concepts related to quadratic equations. These include:

• Definition: A quadratic equation is an equation of the form ax^2 + bx + c = 0, where a, b, and c are real numbers and a ≠ 0.

• Standard Form: Rewriting the quadratic equation in the form ax^2 + bx + c = 0 is essential for solving problems effectively.

• Coefficients: The coefficients a, b, and c represent the numerical values in the quadratic equation.

• Roots: The roots of a quadratic equation are the values of x that satisfy the equation, making ax^2 + bx + c = 0.

Step 2: Identify the Type of Quadratic Equation

Quadratic equations can be categorized into different types based on their roots:

• Real Roots: If the discriminant (b^2 – 4ac) is non-negative, the quadratic equation has real roots, which are distinct or equal.

• Imaginary Roots: If the discriminant is negative, the quadratic equation has complex roots, which involve imaginary unit multiples.

• Repeated Roots: If the discriminant is zero, the quadratic equation has a repeated real root.

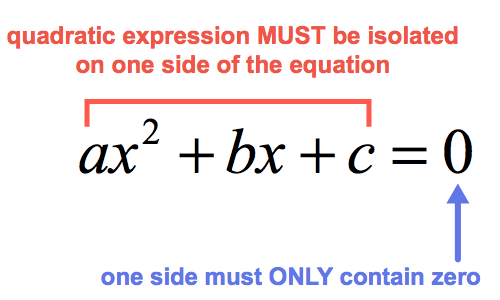
Step 3: Solving Methods

There are three primary methods for solving quadratic equations:

• Factoring: This method involves factoring the quadratic expression ax^2 + bx + c into two linear expressions (a)(b) = 0. The roots are then determined by setting each linear factor equal to zero and solving for x.

• Completing the Square: This method involves converting the quadratic equation into a perfect square trinomial by adding a specific term. The roots are then found by taking the square root of both sides of the equation.

• Quadratic Formula: This formula, x = (-b ± √(b^2 – 4ac)) / (2a), provides a direct method for solving quadratic equations. It can be used for all types of quadratic equations, regardless of the discriminant value.

Step 4: Practice and Application

Regular practice is essential for mastering quadratic equations. Start with simple problems and gradually increase the difficulty level. Apply the learned concepts to real-world scenarios that involve quadratic relationships.

Additional Tips:

• Visualization: Sketching graphs of quadratic equations can provide a visual representation of the roots and their relationship to the equation.

• Pattern Recognition: Observe patterns in the coefficients and roots of quadratic equations to develop shortcuts and problem-solving strategies.

• Technology: Utilize graphing calculators or online tools to verify solutions and explore complex quadratic equations.

Remember, master quadratic equations is a journey, not a destination. Embrace the learning process, seek help when needed, and celebrate your progress along the way. With dedication and perseverance, you’ll become proficient in solving quadratic equations and unlock their applications in various fields.