Let’s learn the vertex form of a quadratic equation and witness the higher dimensions of the quadratic equation. Here in our article, we shall make our discussion on the vertex format of the quadratic equation for the understanding of our readers.
A quadratic equation is an equation that takes the form of ax^2+bx+c=0 and we have to find out the value of unknown. Here x is known as the unknown while a,b and c have their own known values.
Vertex Quadratic Equation
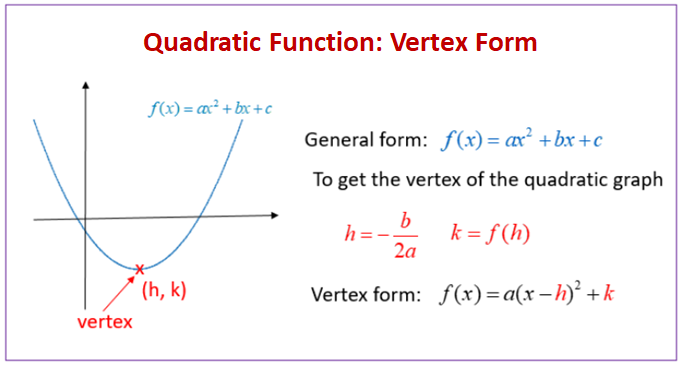
Well, as we know that quadratic equation has the numbers of solving approach. The approach varies as per the complex form of the equation. Vertex format of the quadratic equation is basically the higher level of a quadratic equation for the roots of the equation. The vertex form of the quadratic equation is concerned with the parabola equation in which we use the graph format for the quadratic equation.
The graphic representation of the quadratic equation is actually the parabola form of the equation. So, basically when we need to find out the vertex of the parabola, then we convert the quadratic equation to the vertex format.
In writing a quadratic equation is something that looks like ax^2+bx+c=0 while vertex format looks different. You can represent a vertex quadratic equation as something like y = a(x−h)2+k. Here in both the parabola and vertex form of the quadratic equation, we take y as the “y” coordinate and x as the “x” coordinate.
Furthermore, we take “a” as the constant to decide whether the parabola will open up or down. So, this is how one can draw the vertex form of the quadratic equation to solve the ultimate equation.
Vertex Form of a Quadratic Equation
In most cases, the Vertex format of a quadratic equation is given preference over the parabola format. It generally happens when the parabola form becomes unable to find the roots of quadratic equations. It’s because of the complex form of the equation that requires similar treatment.
So, this is where the vertex format of the quadratic equation takes place for the roots of the equation. You just should know to convert the parabola into the vertex form to find the further coordinates of the equation. Here vertex coordinate looks more simplified in the comparison of the parabola. We definitely recommend learning the vertex form of a quadratic equation to solve the complex form of quadratic equations